| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 강화학습
- update_state
- pinecone
- LangChain
- adaptive_rag
- add_subgraph
- Ai
- 밑바닥부터시작하는딥러닝 #딥러닝 #머신러닝 #신경망
- toolnode
- 밑바닥부터 시작하는 딥러닝
- tool_call_chunks
- summarize_chat_history
- REACT
- Docker
- rag
- Python
- subgraph
- agenticrag
- 강화학습의 수학적 기초와 알고리듬의 이해
- tool_calls
- langgrpah
- 강화학습의 수학적 기초와 알고리듬 이해
- removemessage
- langgraph
- 추천시스템
- chat_history
- fastapi
- conditional_edges
- rl
- RecSys
- Today
- Total
타임트리
[데이콘] 한국에너지공단 전력사용량 예측 AI 경진대회 - 1위 본문

얼마 전 한국에너지공단에서 주최하고 DACON에서 주관한 전력사용량 예측 AI 경진대회에 참여했다. 이 대회의 주제는 전력 수요 예측 시뮬레이션을 통한 효율적인 인공지능 알고리즘을 발굴하는 것으로, 익명화된 건물 정보와 함께 기후 정보를 활용해 60개 건물의 일주일 전력사용량을 매 시간마다 예측하는 문제였다. 팀명을 정하지 않은 채 팀 병합 후 분석을 진행하다 보니 닉네임 j_sean이 그대로 팀명으로 정해졌다. (의도치 않게 j_sean팀의 j_sean으로 참가하게 되었다!)

대학생 시절 데이터 분석 연합 동아리 BITAmin을 통해 알게 된 두 명의 팀원들과 함께 팀장으로 참여했다. 틈틈이 하지만 열심히 참여한 결과, 위와 같이 Modeling 분야에서 1위를 하게 되었다!
따라서 이번 공모전에 참여하면서 배운 점과 느낀 점을 정리하는 것을 시작으로 앞으로 티스토리를 통해 데이터 분석가로 성장하고자 하는 여정을 글로 담아내고자 한다. 첫 게시물을 1위 수상작으로 시작할 수 있어 행복하다.

1. OVERVIEW
(1) 데이터 형태 및 문제 정의
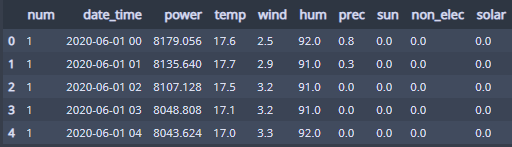
먼저, train set은 60개 건물들의 2020년 6월 1일부터 2020년 8월 24일까지의 데이터로 1시간 단위의 전력사용량(kWh)을 포함하는 기상 관측 데이터로 이루어져 있다. 즉, 다음과 같이 각 건물을 나타내는 건물번호(num), 시간(date_time), 전력사용량(kWh), 기온(℃), 풍속(m/s), 습도(%), 강수량(mm), 일조(hr), 비전기냉방설비운영, 태양광보유 로 이루어져 있다.

test set은 60개 건물들의 2020년 8월 25일부터 2020년 8월 31일까지의 데이터로 train set과 달리 3시간 단위의 예보 데이터가 제공되었다(강수량의 경우 6시간 단위 제공).

num은 1부터 60까지로 건물번호를 의미하는데, train set에는 2040개(85일씩)의 데이터가 60개 각 건물에 대해 존재한다. 또한, test set에는 건물별로 168개 즉, 7일간의 각 건물별 전력사용량을 시간별로 예측해야 하는 시계열 문제라고 할 수 있다.
또한, 추후 변수를 쉽게 다루기 위해 아래와 같이 변수명을 영문으로 변경했다.
|
1
2
3
|
## 변수들을 영문명으로 변경
cols = ['num', 'date_time', 'power', 'temp', 'wind','hum' ,'prec', 'sun', 'non_elec', 'solar']
train.columns = cols
|
cs |
(2) METRIC
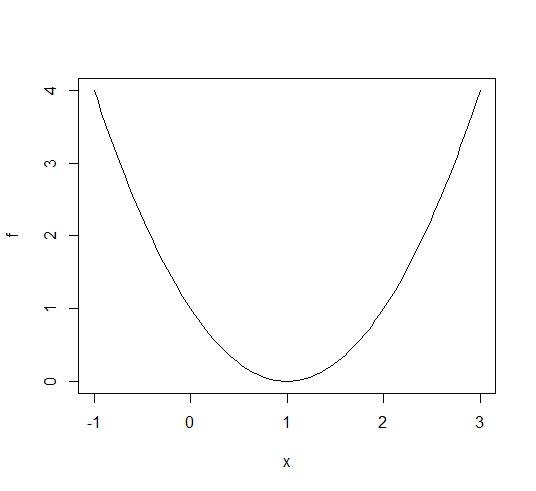
평가지표는 SMAPE(Symmetric Mean Absolute Percentage Error)다. 먼저 SMAPE를 살펴보기에 앞서 SMAPE의 등장 배경인 MAPE를 먼저 살펴보자. MAPE의 수식은 다음과 같다.
$$MAPE=\frac{1}{n}\sum_{i=1}^{n}{|\frac{y_i - \hat{y}_i}{y_i}|}$$
즉, MAPE는 오차($y-\hat{y}$)를 실제값($y$)으로 나눈 뒤 절댓값을 취하고 샘플 수로 나눔으로써 실제값 대비 오차의 비율을 측정한다. 그러나 MAPE는 몇 가지 단점을 가지고 있는데, 첫째는 오차의 절댓값이 같아도 실제값 $y$와 $\hat{y}$의 대소 관계에 따라 값이 달라진다는 것이다(과대추정 값에 더 큰 패널티를 준다). 둘째는 실제값이 0에 가까울수록 동일한 오차여도 더 큰 패널티가 부여되며 특히 실제값이 0일 경우 아예 정의가 되지 않는다!
|
1
2
3
4
5
6
7
|
# Define MAPE loss functon
def MAPE(true, pred):
return np.mean(np.abs((true-pred)/true))
print("실제값이 4일 때 2로 underestimate할 때의 MAPE : {}".format(MAPE(4, 2)))
print("실제값이 2일 때 4로 overestimate할 때의 MAPE : {}".format(MAPE(2, 4)))
print("실제값이 100일 때 98로 underestimate할 때의 MAPE : {}".format(MAPE(100, 98)))
|
cs |
실제값이 4일 때 2로 underestimate할 때의 MAPE : 0.5
실제값이 2일 때 4로 overestimate할 때의 MAPE : 1.0
실제값이 100일 때 98로 underestimate할 때의 MAPE : 0.02
따라서, 이러한 MAPE가 지닌 한계점을 보완하기 위해 SMAPE가 등장한다. SMAPE의 수식은 다음과 같다.
$$SMAPE=\frac{100}{n}\sum_{i=1}^{n}{\frac{|y_i - \hat{y}_i|}{|y_i| +|\hat{y}_i|}}$$
MAPE는 MAPE처럼 동일한 오차일지라도 $y_i$과 $\hat{y}_i$의 대소 관계에 영향을 받지 않는다.
특히 주목할 점은 SMAPE는 MAPE와는 반대로 과소추정에 더 큰 패널티가 부여된다는 점이다. 과소추정보다 과대추정을 용인하는 SMAPE를 사용한 이유에 대해 생각해보자면, 이는 전력을 공급해야 하는 기업 입장에서 생각해보았을 때 실제 필요한 전력량을 정확하게 맞추지 못하고 제대로 공급하지 못해 발생하는 손해보다는 과잉 공급하는 것이 안전한 선택이기 때문이라고 판단했다.
|
1
2
3
4
5
6
7
8
|
# Define SMAPE loss function
def SMAPE(true, pred):
return np.mean((np.abs(true-pred))/(np.abs(true) + np.abs(pred))) * 100
print("실제값이 100일 때 50으로 underestimate할 때의 MAPE : {}".format(MAPE(100, 50)))
print("실제값이 100일 때 150으로 overestimate할 때의 MAPE : {}".format(MAPE(100, 150)))
print("실제값이 100일 때 50으로 underestimate할 때의 SMAPE : {}".format(SMAPE(100, 50)))
print("실제값이 100일 때 150으로 overestimate할 때의 SMAPE : {}".format(SMAPE(100, 150)))
|
cs |
실제값이 100일 때 50으로 underestimate할 때의 MAPE : 0.5
실제값이 100일 때 150으로 overestimate할 때의 MAPE : 0.5
실제값이 100일 때 50으로 underestimate할 때의 SMAPE : 0.5
실제값이 100일 때 150으로 overestimate할 때의 SMAPE : 1.0
이처럼 평가지표를 분석하는 과정까지 정리하는 이유는 이 평가지표를 분석함으로써 얻은 인사이트를 추후 모델링 과정에 적용함으로써 성능을 크게 끌어올릴 수 있었기 때문이다.
또한, 익명화된 건물의 위치, 용도 등을 알 수 없었기 때문에 하나의 모델로 각 건물을 예측하는 것보다는 모델링을 함에 있어 각 건물별로 모형의 하이퍼 파라미터를 튜닝함으로써 각 건물별에 맞는 모델을 적합하기로 결정했다.
2. Preprocessing
앞서 문제 정의에서 보듯, 이번 데이터는 시간에 종속적인 전력사용량을 예측하는 문제로 시계열과 관련 깊다. 아래 그림은 12번째 건물의 전력사용량 그래프이다. 주기성과 함께 약간의 추세가 보이고, 변동이 시간에 따라 증가하므로 승법 모형이 적합한 듯한 모습이 인다. 따라서, 전통적 통계 방법인 ARIMA, ARIMAX를 비롯한 facebook에서 배포한 라이브러리인 fbprophet 등을 사용해보았으나 SMAPE 기준 성능이 좋지 못했다.
따라서 시간을 나타내는 변수들을 최대한 회귀 도메인으로 끌고 오기 위해 노력했다. 이번 대회에서 주목할 만한 전처리는 크게 3가지로 다음과 같다. (시계열에서의 자기 회귀(Auto Regression)를 반영하는 lag 변수도 시도하였으나 그리 좋지 못했다. 아무래도 목표가 예측이므로 평가기준 성능을 기준으로 변수들을 선택했다.)

1. date_time 변수를 월(month), 요일(weekday), 년도기준주차(week), 시간(hour) 변수로 범주화했다. 여기서 시간 변수는 주기를 가지므로 sin time & cos time으로 cyclical encoding 하여 추가 후 삭제했다. 또한, 주말을 나타내는 변수에 2020년 8월 17일은 광복적 임시공휴일이므로 휴일을 나타내는 변수 holiday를 추가했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# 시간 관련 변수들 생성
date = pd.to_datetime(train.date_time)
train['hour'] = date.dt.hour
train['day'] = date.dt.weekday
train['month'] = date.dt.month
train['week'] = date.dt.weekofyear
### 공휴일 변수 추가
train['holiday'] = train.apply(lambda x : 0 if x['day']<5 else 1, axis = 1)
train.loc[('2020-08-17'<=train.date_time)&(train.date_time<'2020-08-18'), 'holiday'] = 1
## cyclical encoding
train['sin_time'] = np.sin(2*np.pi*train.hour/24)
train['cos_time'] = np.cos(2*np.pi*train.hour/24)
|
cs |
2. 각 건물의 전력사용량별 특징을 잡아내기 위해 아래와 같은 전력사용량 평균 변수들 및 표준편차 변수를 각각 생성하였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
#######################################
## 건물별, 요일별, 시간별 발전량 평균 넣어주기
#######################################
power_mean = pd.pivot_table(train, values = 'power', index = ['num', 'hour', 'day'], aggfunc = np.mean).reset_index()
tqdm.pandas()
train['day_hour_mean'] = train.progress_apply(lambda x : power_mean.loc[(power_mean.num == x['num']) & (power_mean.hour == x['hour']) & (power_mean.day == x['day']) ,'power'].values[0], axis = 1)
#######################################
## 건물별 시간별 발전량 평균 넣어주기
#######################################
power_hour_mean = pd.pivot_table(train, values = 'power', index = ['num', 'hour'], aggfunc = np.mean).reset_index()
tqdm.pandas()
train['hour_mean'] = train.progress_apply(lambda x : power_hour_mean.loc[(power_hour_mean.num == x['num']) & (power_hour_mean.hour == x['hour']) ,'power'].values[0], axis = 1)
#######################################
## 건물별 시간별 발전량 표준편차 넣어주기
#######################################
power_hour_std = pd.pivot_table(train, values = 'power', index = ['num', 'hour'], aggfunc = np.std).reset_index()
tqdm.pandas()
train['hour_std'] = train.progress_apply(lambda x : power_hour_std.loc[(power_hour_std.num == x['num']) & (power_hour_std.hour == x['hour']) ,'power'].values[0], axis = 1)
|
cs |
3. 전력사용량과 연관을 가질만한 불쾌지수(THI; Temperature and Humidity Index)와 냉방도일(CDH; Cooling Degree Hour) 변수를 추가했다(데이콘 코드공유 - 동준이 : https://dacon.io/competitions/official/235736/codeshare/2743?page=1&dtype=recent). 여기서 냉방도일이란 날씨의 더운 정도를 나타내는 지수로 냉방도일 값이 크다는 것은 기후가 덥고 냉방을 위해 전력이 많이 소모된다는 것을 의미한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
## ref: https://dacon.io/competitions/official/235736/codeshare/2743?page=1&dtype=recent
train['THI'] = 9/5*train['temp'] - 0.55*(1-train['hum']/100)*(9/5*train['hum']-26)+32
def CDH(xs):
ys = []
for i in range(len(xs)):
if i < 11:
ys.append(np.sum(xs[:(i+1)]-26))
else:
ys.append(np.sum(xs[(i-11):(i+1)]-26))
return np.array(ys)
cdhs = np.array([])
for num in range(1,61,1):
temp = train[train['num'] == num]
cdh = CDH(temp['temp'].values)
cdhs = np.concatenate([cdhs, cdh])
train['CDH'] = cdhs
|
cs |
마지막으로 모든 값이 0으로 동일한 비전기냉방설비운영, 태양광보유와 같이 모델링에 사용하지 않을 변수들을 제거한 뒤의 최종 train set의 첫 5행은 다음과 같다.

Test set 역시 train set과 동일한 과정으로 전처리하였는데, 기후 변수는 3시간(강수량의 경우 6시간) 단위의 예보 데이터이므로 pandas의 interpolate() 메서드를 이용해 선형 보간하였다.
3. Modeling
- XGBoost with customized loss function
데이터 분석에는 크게 2가지 목적이 있다고 생각한다. 하나는 설명력, 또 하나는 예측력이다. 두 가지 목적은 모두 취할 수 없는 반비례 관계에 놓여있다. 이번 분석의 목표는 최대한의 예측력을 끌어올리는 것이 목적이며, 시계열 도메인에서 회귀 도메인으로 변환하였기에 모델을 고려할 때 머신러닝 기법 중 트리 기반 부스팅 모형들을 사용하기로 결정했다. 우선 예측해야 하는 기간은 일주일 즉 168(=24*7)시간이기에 test set과 가장 가까운 마지막 일주일을 validation set으로 설정하고 그 이전까지의 데이터를 train set으로 나누었다. 그리고 각 건물별 XGBoost, LightGBM, 그리고 CatBoost 모형을 디폴트 및 간단한 그리드 서치로 찾은 하이퍼 파라미터로 성능을 평가한 결과 XGBoost가 가장 좋은 성능을 보여주었다. 따라서, XGBoost를 이용해 모형을 적합하기로 결정했다.
여기서 가장 주목할만한 점이자 이번 분석을 통해 새로 시도한 부분은 모형 학습 시의 손실함수(loss function)을 customizing했다는 것이다. 앞서 평가지표에서 살펴보았듯 이번 평가지표 SMAPE는 과소추정에 대한 패널티가 크다. 따라서, 모델이 전력사용량을 과소추정하지 않도록 학습시키고자 다음과 같이 MSE를 살짝 변형한 weighted MSE를 정의했다. 코드를 살펴보면, $y_i - \hat{y}_i$로 정의한 잔차(residual)가 0보다 크다면 즉, 과소추정이라면 그레디언트에 $\alpha$를 곱해줌으로써 패널티의 크기를 조절할 수 있다. 만약 $\alpha=1$이라면, 통상의 MSE와 동일하다.
|
1
2
3
4
5
6
7
8
|
# custom objective function for forcing model not to underestimate
def weighted_mse(alpha = 1):
def weighted_mse_fixed(label, pred):
residual = (label - pred).astype("float")
grad = np.where(residual>0, -2*alpha*residual, -2*residual)
hess = np.where(residual>0, 2*alpha, 2.0)
return grad, hess
return weighted_mse_fixed
|
cs |
앞서 정의한 weighted MSE를 목적함수로 하여 XGBoost 회귀 모델을 적합한 예는 아래와 같다. 일반적인 MSE를 사용했을 경우보다 weighted MSE를 사용한 경우, SMAPE가 낮아지는 것을 확인할 수 있다. 그래프에서 초록색이 나타내는 선이 validation set에 대한 예측값을 나타낸다.


이렇게 정의한 loss function을 사용해 XGBoost 회귀 모델의 하이퍼 파라미터를 튜닝했다($\alpha=100$으로 고정). 그 후 best_iteration을 찾았으며, 마지막으로 다시 한 번 weighted MSE 내의 $\alpha$를 튜닝했다. 이때, 앞서 언급한 마지막 일주일을 제외한 train 데이터로 마지막 일주일을 평가하는 hold-out 방식을 이용했다.
- Prediction
이렇게 찾은 하이퍼 파라미터들을 train set과 validation set을 합친 전체 데이터에 대해 최종적으로 재적합했다. 그리고 예측에 있어 seed의 영향을 제거하고 보다 robust하게 만들기 위해 6개 seed 값으로 적합한 XGBoost 회귀 모형의 예측값을 평균을 취했다. 그 결과 중 일부의 그래프는 다음과 같다.

4. Post-processing
customized loss function과 더불어 이번 분석에서 주요했던 건 예측값에 대한 후처리였다. 이 역시 예측 시 SMAPE 평가지표의 특성을 반영하기 위한 노력이었다. 이는 각 건물의 시간대별 예측해야 하는 시점 대비 4주 전까지의 전력 사용량 최솟값을 사용하는 방식으로 진행했다. 즉, 특정 건물의 특정 시간에 대한 전력 사용량 예측값이 4주 전까지의 전력사용량의 최솟값보다 작다면 이를 대체하는 방식이다. 이러한 방법이 가능한 이유로, 주어진 데이터가 6월에서 8월까지의 데이터로 초여름 - 한여름까지로 한정되어 있으며 예측하는 시기가 8월의 마지막 주였으며, 전력사용량이 증가하는 추세를 반영한 것이다([그림 1] 참고).
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
df = pd.read_csv('./submission/submission.csv')
for i in range(60):
min_data = train_to_post.loc[train_to_post.num == i+1, ].iloc[-28*24:, :] ## 건물별로 직전 28일의 데이터 불러오기
min_data = pd.pivot_table(min_data, values = 'power', index = ['day', 'hour'], aggfunc = min).reset_index()
pred = df.answer[168*i:168*(i+1)].reset_index(drop=True) ## 168개 데이터, 즉 건물별 예측값 불러오기
day = test_to_post.day[168*i:168*(i+1)].reset_index(drop=True) ## 예측값 요일 불러오기
hour = test_to_post.hour[168*i:168*(i+1)].reset_index(drop=True) ## 예측값 시간 불러오기
df_pred = pd.concat([pred, day, hour], axis = 1)
df_pred.columns = ['pred', 'day', 'hour']
for j in range(len(df_pred)):
min_power = min_data.loc[(min_data.day == df_pred.day[j])&(min_data.hour == df_pred.hour[j]), 'power'].values[0]
if df_pred.pred[j] < min_power:
pred_clip.append(min_power)
else:
pred_clip.append(df_pred.pred[j])
|
cs |
이처럼 후처리한 데이터는 대회가 끝나고 난 뒤 확인한 private score에서 가장 결정적인 역할을 했다. 대부분의 건물에서는 크게 변화된 값은 없었으나 몇 개 건물에 있어서는 꽤나 크게 값이 변경되었다. 그 효과는 아래 그래프에서 확인할 수 있다.


5. 마치며
이번 경진대회에 참여하며 크게 2가지를 배웠다. 첫째는 대회의 평가지표를 이해하는 것이다. 이를 통해 모델링 과정에서 loss function을 customizing 하는 방법을 경험했다. 둘째는 모델링 과정에서의 논리성이다. 이전에는 논리적인 과정 없이 이것저것 닥치는 대로 변수를 생성하고 제거하고, 모델 역시 큰 고민 없이 무작정 돌려보는 등 분석이라고 칭하기 부끄러운 정도였다. 그러나 이번 대회를 통해 무작정 시도하는 것이 아니라, 주어진 문제를 고민하고 어떤 변수가 어떻게 의미가 있는지 논리적으로 전개해나가는 과정을 배울 수 있었다.
또한 처음으로 경진대회에서 입상한 경험이자 1등이라는 결과를 얻을 수 있어서 다행이다. 아무래도 혼자서 했으면 몇 가지 생각에만 갇혀 이런 성과를 얻지 못했을 것 같다. 같이 한 팀원들에게 고맙다는 말을 하고 싶다. 앞으로 더 공부하고 많이 참여하며 여러 문제들을 풀어보고 싶다.