| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- agenticrag
- Ai
- langgraph
- pinecone
- 밑바닥부터시작하는딥러닝 #딥러닝 #머신러닝 #신경망
- chat_history
- tool_call_chunks
- conditional_edges
- tool_calls
- Docker
- 강화학습의 수학적 기초와 알고리듬 이해
- removemessage
- 강화학습
- rag
- LangChain
- adaptive_rag
- add_subgraph
- fastapi
- subgraph
- 추천시스템
- 밑바닥부터 시작하는 딥러닝
- update_state
- Python
- REACT
- RecSys
- langgrpah
- rl
- 강화학습의 수학적 기초와 알고리듬의 이해
- toolnode
- summarize_chat_history
- Today
- Total
타임트리
Week5. MDP-1 본문
앞서 학습한 확정적 동적계획법, 확률 과정, 마르코프 프로세스, 마르코프 보상 프로세스는 궁극적으로 마르코프 의사결정 프로세스(Markov Decision Processes: MDP)를 소개하기 위함이었다. 이번 주차에서는 MDP 모델이 무엇인지, 그리고구성요소에 대해 알아보자.
1. 마르코프 의사결정 프로세스 (MDP)
동적계획법은 확정적 동적계획법과 확률적 동적계획법으로 나눠지며, MDP는 확률적 동적계획법의 special case라고 볼 수 있다. 확정적 동적계획법은 앞선 주차에서 학습한 내용처럼 특정 상태에서 행동의 결과가 어떤 상태로 전이될지 이미 알려져있고, 그 상태로만 확정적으로 전이가 된다. 하지만, 확률적 동적계획법은 어떤 상태에서 행동을 취했을 때 다음 상태가 확률적으로 결정되는 경우에 해당한다. 즉, MDP 역시 agent가 특정 state에서 특정 action을 취했을 때 다음 state는 확률적으로 정해진다.
MDP는 일종의 확률과정이지만, 일반적인 확률과정과 달리 시스템 변화를 야기하는 의사결정이 포함되어 있다. 확률과정, 특히 MP와 MRP에서는 상태 간 전이가 이미 정의한 상태 전이확률에 의해서 이루어졌다. 하지만, MDP는 일종의 동적계획법으로 순차적으로 의사결정을 하는 메커니즘이 적용된다. agent가 존재하여 state를 관찰하고 action을 취하면 그 이후의 확률과정이 영향을 받는다. 이때, agent는 확률과정 상의 state와 선택한 action에 따른 일련의 보상을 얻게 된다. 정리하면 다음과 같다.

- MDP는 순차적으로 의사결정을 내리는 매커니즘이 적용되고, 의사결정이 프로세스에 영향을 미친다.
- agent가 특정 state에서 특정 action을 취하면, 다음 state가 확률적으로 결정된다.
- agent는 state와 action에 따른 일련의 보상을 얻게 된다.
2. MDP의 구성요소
MDP는 의사결정 시점 $T$, 상태공간 $S$, 행동공간 $A_s$, 상태전이확률 $p_t(s^\prime|s,a)$, 보상 $r_t(s,a)$, 그리고 감가율 $\gamma$로 구성되어 있으며, 다음과 같이 표현할 수 있다.
MDP $$\{T,S,A_s,p_t(\cdot|s,a),r_t(s,a),\gamma:~t \in T, s \in S, a \in A_s\}$$
- $T \in [0,\infty)$ - 의사결정 시점(decision epoch)들의 집합
- MDP에서는 순차적 의사결정 상황에서 의사결정자가 의사결정을 하고 행동을 취하는 시점(MP에서는 시스템 상태 관찰 시점)
- $T$가 이산형이면, 단계(stage)들의 집합
- $T$가 finite이면 finie-horizon MDP으로 마지막 의사결정 시점에서는 의사결정이 없으며, infinite이면 infinite-horizon MDP로 구분
- $S$: 상태공간(state space) - 확률과정이 취하는 값들의 집합
- 환경(environment)에서부터 관찰이 가능한, 의사결정에 필요한 최소한의 정보들의 집합
- 주로 $S$가 이산형 값들의 집합인 경우를 다룸
- $A_s$: 행동공간(action space) - 상태가 $s \in S$일 때 가능한 행동(action)들의 집합
- 상태 $s$에 따라 취할 수 있는 action이 다를 수 있음
- 즉, 행동은 상태 $s$에 의존적임
- $p_t(s^`|s,a)$: 상태전이확률(state transition probabilities)
- 동적계획법이 확정적인지 확률적인지 차이를 만드는 요소
- 현재 상태 $s$에서 행동 $a$를 취할 때, 다음 의사결정 시점의 상태 $s^\prime$가 어떻게 될지를 규정
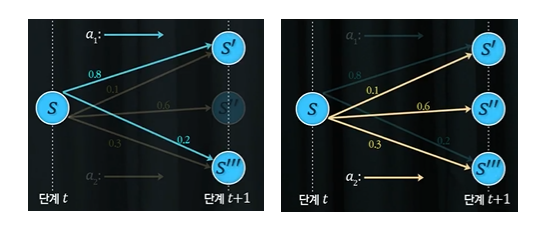
위 예시를 살펴보며 상태전이확률에 대해 살펴보자. 현재 agent가 $t$시점에 $S$ 상태에 놓여 있다고 하자. 상태 $S$에서는 가능한 행동이 $a_1$과 $a_2$가 있다. 위 그림에 따르면, 상태전이확률은 다음과 같이 정의가 되어있다. $$p(S^\prime|S, a_1)=0.8, p(S^{\prime\prime\prime}|S,a_1)=0.2, p(S^\prime|S, a_2)=0.1, p(S^{\prime\prime}|S,a_2)=0.6, p(S^{\prime\prime\prime}|S,a_2)=0.3$$
즉, 똑같은 시점과 똑같은 상태지만, $a_1$이라는 action을 취할 때와 $a_2$라는 action을 취할 때 각각 다음 시점에 놓이는 상태가 다르며, 이는 각 action에 따라 확률적으로 주어져있다. 다시 말해, 프로세스가 상태전이확률에 따라 진행이 되고 있다는 사실을 알 수 있다.
"현재 state에서 어떤 action을 취했을 때 다음 상태가 확률적으로 결정된다"를 이해하기 위해 자율주행 자동차가 현재 상태에서 어떤 action을 취할 지 결정하는 상황을 생각해보자. 이때 만약 다음 상태가 확정적이라면, 자동차가 어디로 이동하면 '그 다음 상황은 이렇게 될거야'라고 사전에 이미 알고 있고 그대로 실행된다. 하지만, 확률적인 상황에서는 미처 인지하지 못한 사물과 충돌하는 등 내가 기대했던 상태와는 또 다른 상태로 변할 수 있다. 즉, 확률적이라는 의미는 이러한 불확실성이 존재하는 것이다.
- $r_t(s,a)$: 보상(rewards)
- 의사결정시점 $t$에서 상태가 $s$일 때, 행동 $a$를 취함으로써 환경으로부터 얻게되는 보상의 기대값(MRP에서는 어떤 상태에 진입하기만 하면 보상이 주어졌었음)
- 상태 $s$에서 행동 $a$를 취해 다음 상태 $s^\prime$에 도달해 보상이 주어지는 경우도 존재. 이 경우 상태전이확률을 알고 있으므로 보상은 아래와 같이 계산 가능
- $r_t(s,a) = \sum_{s^\prime \in S}{p_t(s^\prime|s,a)r_t(s,a,s^\prime)}$
- $r_N(s)$: finite-horizon MDP에서 마지막 단계가 $N$일 때, 상태 $s$에서 종료 시 취득하게 되는 보상(terminal reward) - infinite-horizon MDP에서는 정의할 필요 없음
- $\gamma$: 감가율(discount factor) - 미래의 보상을 현재의 가치로 환산
- 현재의 보상이 미래의 보상보다 가치가 높다는 개념
- 즉, 미래의 보상은 현재의 보상보다 가치가 낮다를 의미하는 개념
- 미래에 받게 될 보상에 대한 불확실성을 고려한 신뢰도를 표현

3. MDP 정책(Policy)
time space $T$, state space $S$, action space $A_s$, trainsition probability $p_t(s^\prime|s,a)$, reward $r_t(s,a)$, discount factor $\gamma$가 정의되면 이제 MDP의 정의는 끝났다고 볼 수 있다. 그럼, MDP를 통해서 우리가 얻고자 하는 것을 상기해보자. 우리는 MDP를 통해 매 단계마다 어떤 상태에서 어떤 행동을 취해야지 원하는 결과(보상합 최대화)를 얻을 수 있을지 알아내는 것이다.
의사결정규칙(decision rule) $\delta$
각 단계 별로 특정 상태에서는 어떤 행동을 취해야할지 나타내는 규칙을 의사결정 규칙(decision rule) $\delta_t$라고 하며, 시간 $t$에 의존한다.
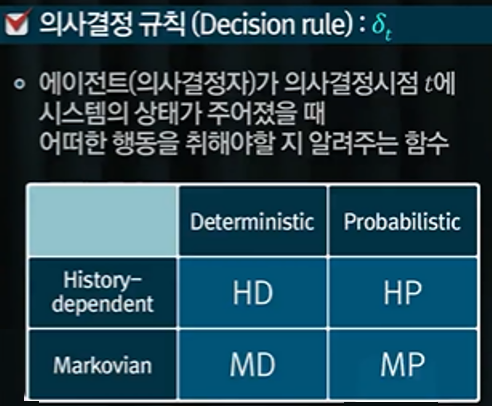
의사결정 규칙은 위 표와 같이 나눠볼 수 있는데, 각 행 또는 열의 의미는 다음과 같다.
- History-dependent: 과거의 모든 이력을 입력받아 다음 행동을 출력
- Markovian: 현재 상태만으로 다음 행동을 출력
- Deterministic: 어떤 행동을 확정해 제시
- Probabilistic: 어떤 행동을 확률적으로 제시
우리는 주로 Markovian 의사결정 규칙에 관심을 가질 것이다. 즉, 과거의 이력은 상관 없고 현재 상태를 입력값으로 했을 때 내가 취할 행동이 무엇인지를 알려주는 의사결정에 관심을 갖는다. Markovian-Deterministic(MD)의 경우, 의사결정규칙은 $\delta_t(s)$로 상태가 주어지면 선택할 수 있는 행동 중 하나를 반환한다. 반면, Markovian-Probabilistic(MP)의 경우, 의사결정규칙의 형태는 $\delta_t(a|s)$로 어떤 상태가 주어졌을 때 행동에 대한 확률을 반환해준다. 여기서 짚고 넘어갈 점은, 확률적인 의사결정 규칙이 강화학습 매커니즘 설계시 유리하다는 점이다.
정책(policy) $\pi$
정책은 의사결정 규칙의 집합이다.
- 모든 의사결정 시점에서의 일련의 의사결정 규칙들인 $\delta_1, \delta_2, \delta_3, \cdots$의 집합
- 만약 모든 의사결정 시점에서 동일한 의사결정 규칙이 적용된다면, 정책 $\pi$가 안정적(stationary)이라고 부름
- $\pi \equiv \delta^{\infty}$
의사결정시점들의 집합인 시간공간 $T$를 정의할 때, 시간공간이 유한하면 finite-horizon MDP, 무한하면 infinite-horizon MDP라고 부른다고 언급했다. 후에 학습하겠지만, 강화학습의 근거가 되는 MDP 모델은 infinite-horizon MDP이다. 이런 경우 기본적으로 관심 있는 정책은 모든 의사결정 규칙이 적용되는 안정적인 정책(stationary policy)이다.
4. MDP 예시 1 - 주사위 던지기 게임
다음과 같은 주사위 던지기 게임을 가정하고, MDP의 구성요소를 정의해보자.
- 게임 규칙
- 매 라운드마다, go 또는 stop
- 만약 stop을 선택하면, $8를 받고 게임 종료
- 만약 go를 선택하면, $4를 받고 주사위 던짐
- 만약 주사위가 1 또는 2라면 게임 종료
- 3,4,5,6이라면 다음 라운드 진행 가능
1) Time space $T=\{1,2,3,\cdots\}$: 매 라운드마다 의사결정 시점을 내려야 하므로, 매 라운드가 의사결정 시점의 집합
2) State space $S=\{in, end\}$: 게임을 진행 중인 상태와 게임이 종료된 상태가 존재
3) Action space $A_{in}=\{go, stop\}, A_{end} = \{stop\}$: 상태 $s$에서 go, 또는 stop을 결정
4) State trainsition probability: 이전 상태의 이력은 중요하지 않음.현재 어느 상태에 있는지가 중요하므로 마르코프 성질을 만족함.

5) rewards: 어떤 상태에서 어떤 행동을 취했을 때 얻을 수 있는 보상의 기댓값
$$r_t(in,stop) = \$8, r_t(in,go) = \$4, r_t(end,stop)= \$0$$
위처럼 정의한 MDP를 파악하기 쉽게 상태전이다이어그램으로 나타내보자. 좌측 그림처럼 표현할 수도 있지만, 우측 그래프처럼 임시적인 노드인 찬스 노드(chance node)를 추가하여 조금 더 알아보기 쉽게 표기할 수 있다. 찬스 노드 (IN,go)를 봐보자. 우선 어떤 상태에서 특정 행동을 취하면 우선 찬스 노드로 전이가 된다. 그 다음 찬스노드에서 확률적으로 다음 상태로 분기가 이루어진다. (IN,go)가 주어진 상황에서 1/3의 확률로 END 상태로 전이가 되고 1/3의 확률로 IN 상태로 전이가 이루어진다. 그리고 이때의 보상은 모두 \$4가 된다. 이렇게 표기했을 때의 표현방식에 따르면 $r_t(IN,go,IN)=\$4$으로 나타낼 수 있다.

'Reinforcement Learning > 강화학습의 수학적 기초와 알고리듬 이해' 카테고리의 다른 글
| Week7. MDP-3 (0) | 2022.04.06 |
|---|---|
| Week6. MDP-2 (0) | 2022.04.03 |
| Week4. 마르코프 과정 (0) | 2022.03.31 |
| Week3. 동적계획법2 (0) | 2022.03.29 |
| Week2. 동적계획법1 (0) | 2022.03.27 |