| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- fastapi
- agenticrag
- summarize_chat_history
- langgraph
- 강화학습의 수학적 기초와 알고리듬의 이해
- tool_call_chunks
- rl
- tool_calls
- pinecone
- REACT
- 추천시스템
- toolnode
- conditional_edges
- subgraph
- 밑바닥부터 시작하는 딥러닝
- adaptive_rag
- chat_history
- Docker
- langgrpah
- removemessage
- LangChain
- 강화학습
- Ai
- rag
- update_state
- Python
- 밑바닥부터시작하는딥러닝 #딥러닝 #머신러닝 #신경망
- 강화학습의 수학적 기초와 알고리듬 이해
- RecSys
- add_subgraph
- Today
- Total
타임트리
Week3. 동적계획법2 본문
최단 경로 문제(Shortest path problem)
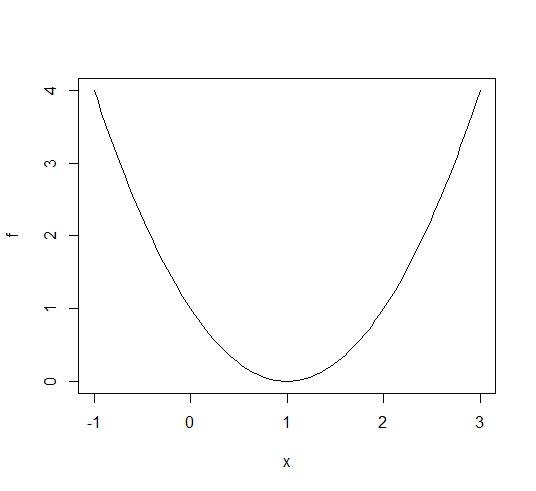
아래 그림과 같이 1번 노드에서 10번 노드까지 최단 거리를 찾는 문제를 생각해보자.

우선 그래프를 살펴보자. 노드끼리 이어진 선은 아크(arc)라고 하며, 화살표(→)로 표시한 아크는 일방통행, 선으로만 표시된 아크는 양방통행을 나타낸다. 또한 아크 옆에 표시된 숫자는 노드에서 노드로 이동까지의 거리 혹은 소요되는 시간으로 볼 수 있다. 여기서는 거리라고 하자.
위와 같은 상황에서 1번 노드에서 10번 노드까지 가장 빨리 이동하는 경로를 찾기 위해서는 어떻게 해야할까? 먼저 가장 단순한 방법은 모든 경로에 대한 거리를 계산하고 비교하는 것이다. 그러나 이 방법은 비효율적이란 걸 금방 알아차릴 수 있다. 이 문제를 동적계획법으로 해결해보자.
동적계획법을 적용하기 위해서는 크게 2가지에 대한 정의가 필요하다. 첫 번째는 상태, 행동에 대한 정의, 두 번째는 재귀식을 통한 가치 함수를 정의하는 것이다. 차례대로 살펴보자.
상태, 행동에 대한 정의
상태(state)는 의사결정을 내리기 위해 필요한 최소한의 정보를 말한다. 순차적인 의사결정의 과정(단계)은 각 노드에서 이루어진다. 따라서, 상태 정보는 현재 노드의 위치가 될 것이다. 자연스럽게 상태를 바탕으로 이루어지는 의사결정인 행동은 다음으로 이동할 노드가 무엇인지가 될 것이다.
- 상태: 현재 위치한 노드
- 행동: 다음으로 이동할 노드
재귀식을 통한 가치 함수 결정
앞서 정의한 상태와 행동을 기반으로 최적화 원리(principle of optimality)를 만족하는 재귀식(recursive equation)을 결정해야 하며 이러한 재귀식을 가치 함수(value function)라고 한다. 아래의 예시를 바탕으로 가치 함수를 도출해보자.

1번 노드에서 출발해 X 노드로 도착하는 문제에서 현재 1번 노드에 위치해 있을 때(상태), 2번, 3번, 4번 노드 중 어떤 노드로 이동해야할까(행동)? 위 그래프가 주어져있다면, 당연히 X 노드까지의 거리가 가장 짧은 2번 노드를 선택할 것이다. 1번 노드에서 2번, 3번, 4번 각각의 노드까지의 거리는 5, 2, 11이며, 각각의 노드부터 X 노드까지의 최단 거리는 20, 25, 17이다. 따라서, 2번, 3번, 4번 각각의 노드를 선택했을 때 1번부터 X 노드까지의 총 소요시간은 25, 27, 28이기 때문에 2번 노드를 선택했을 때 최단 거리가 된다. 이러한 의사결정을 내릴 수 있던 이유는 행동을 선택한 이후의 노드부터 종점까지의 최단 소요시간을 알고 있기 때문이다. 이러한 의사결정의 과정을 참고하여, 가치 함수를 도출해보자.
우선, 가치 함수는 상태에 대한 함수로써 $v^*$로 표현한다. 즉, 최단 거리 문제에서의 가치 함수 $v^*(s_t)$는 다음과 같이 정의할 수 있다.
$v^*(s_t) :=$현재 노드에서 종점까지 최단 거리에 해당하는 거리
위 그래프에서의 의사결정을 내린 과정을 살펴보면, 현재 위치부터 다음 위치까지의 거리와 다음 상태에서 종점까지 최단 거리에 해당하는 거리를 더해 비교했다. 즉, 다음과 같이 가치 함수를 만들 수 있다.
$$v^*(s_t) = \underset{s_{t+1}}{\min}{\{r(s_t, s_{t+1}) + v(s_{t+1})\}}$$
문제 풀이
그럼 문제를 풀어보자. 아래처럼 표가 주어졌을 때 직접 계산해보면 모든 값이 도출되는 것을 확인할 수 있다.
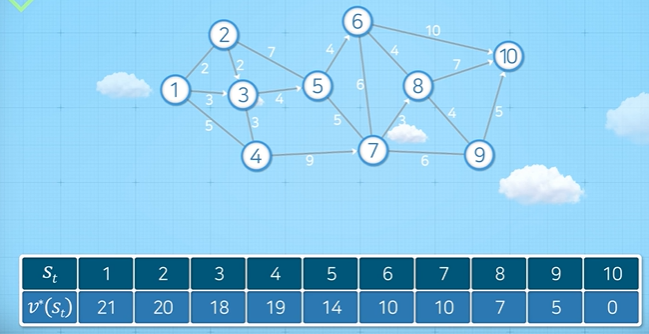
예를 들어, $v(8) = \min{\{4+10, 7+0, 4+5\}}=7$ ($s_{t+1}$이 각각 6번 노드, 10번 노드, 9번 노드일 때) 처럼 계산할 수 있다.
사실 여기엔 한 가지 문제가 있다. 만약 위와 같이 표가 주어지지 않았다면, 재귀식을 통해 문제를 해결할 수 없다. 재귀식이 만족되기 위해서는 하위 문제를 풀 수 있어야 한다. 그러나, 표가 주어지지 않은 상황에서 $v(8)$을 계산하기 위해서는 $v(6), v(10), v(9)$이 필요하다. 그런데, $v(9)$를 계산하기 위해서는 $v(10), v(8), v(7)$이 필요하다. 즉, $v(8)$을 계산하기 위해서 $v(9)$가, $v(9)$를 계산하기 위해선 $v(8)$이 필요한 모순이 생긴다.
이러한 상황을 순환 참조 상황이 발생했다고 하며, 동적계획법에 기반해 문제를 해결할 수 없다. 이를 해결하기 위해서는 상태에 대해 재정의를 해야 한다. 즉, 현재 상태 정보만으로는 재귀식을 도출하기 어렵다고 해석해야 하며, 추가적인 정보를 포함한 상태를 재정의 후 재귀식을 도출해야 한다.
그러나, 이 부분은 현재 수업 내용의 범위를 벗어나기 때문에 현재 내가 어느 노드에 있는지라는 상태만으로 문제 해결이 가능한 다음 예시를 살펴보자.
Stagecoach 문제
앞서 순환 참조 상황이 발생한 이유는 양방통행이 가능했기 때문인데, stagecoach 문제는 최단 경로에서도 일방통행만이 존재하는 특별한 경우를 의미한다. 그래서 앞서 정의한 재귀식만으로 문제 해결이 가능하다.

위 그림을 보면, A 노드에서 J 노드까지 최단 경로를 찾고자 할 때, 상태 $s_t$는 현재 위치, 행동 $a_t$는 다음 노드의 위치다. 이를 바탕으로 상태함수를 앞선 문제와 동일하게 도출할 수 있다. 즉, $v^*(s_t)$는 노드 $s_t$에서 목적지 J까지의 최소 소요시간을 의미한다. 식을 구체적으로 살펴보면 $r_t(s_t,a_t) + v^*(s_{t+1})$은 현재 노드에서 다음 노드로 이동할 때 거리와 그 다음 노드에서부터 J 노드까지의 최소 거리의 합을 의미한다. 여기에 $min$의 의미는 그러한 거리의 합이 최소화 되는 $a_t$를 선택하도록 한다.
$v$값을 계산하기 위해서는 어떻게 해야할까? 역진귀납법을 통해 목적지와 가장 가까운 노드부터 순차적으로 문제를 해결하면 된다. 구체적으로, $v$값을 계산해보자.
먼저 Stage4를 구해보자. $H$에서 취할 수 있는 행동은 J로의 이동밖에 없고, J 노드에서의 가치 함수는 0이므로, $v(H)=3$이다. 마찬가지로 $v(I)=4$다. 따라서, $v^*(H) = 3, v^*(I)=4$ 이다.

다음으로 Stage3을 보자. $E$에서 취할 수 있는 행동은 H와 I 두 가지가 있으며 가치 함수를 구해보면, $v(E)=\min{\{1+3, 4+4\}}=4$이므로, $s_t=E$일 때 행동 H를 선택해야 최소 거리를 만족한다. 마찬가지로, $F$에서 취할 수 있는 행동은 H와 I 두 가지가 있으며 가치 함수를 구해보면, $v(F)=\min{\{6+3, 3+4\}}=7$이므로, $s_t=F$일 때 행동 I를 선택해야 최소 거리를 만족한다. 이러한 과정을 반복하면 다음과 같은 표를 얻을 수 있다.
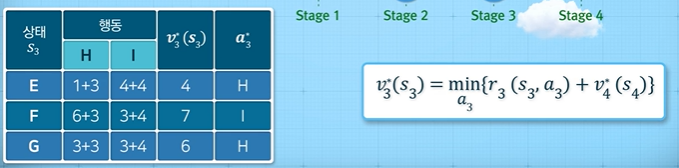
다음으로 Stage2를 보자. $B$에서 취할 수 있는 행동은 E, F, G 세 가지가 있으며 가치 함수를 구해보면, $v(B)=\min{\{7+4, 4+7, 6+6\}}=11$이므로, $s_t=B$일 때 행동 E 또는 F를 선택해야 최소 거리를 만족한다.

우리의 목적은 궁극적으로 $v(A)$를 구하는 것이다. 앞에서와 마찬가지로 $A$에서 취할 수 있는 행동은 B, C, D 세 가지가 있으며, $v(A)=\min{\{2+11, 4+7, 3+8\}}=11$이므로 $s_t=A$일 때 행동 C 또는 D를 선택해야 최소 거리를 만족한다.

그럼 노드 A부터 J까지 구체적인 최단 경로는 어떻게 찾을까? 예를 들어, A에서 C를 선택했다고 하자. 그러면 (A → C → E → H → J)가 최단 경로가 될 것이다. 혹은 (A → D → E → H → J), (A → D → F → I → J)도 가능하다.
방문판매원 문제(Traveling Salesman Problem, TSP)
방문판매원 문제는 여러 개의 도시와 그 도시 간의 거리가 주어졌을 때, 각 도시를 정확히 한 번씩만 방문해 원래 도시로 돌아오는 가장 짧은 경로를 찾는 문제를 일컫는다. 외판원 문제가에 대해 가치 함수의 기반한 재귀식을 도출해보자. 주어진 행렬은 4개 도시가 주어졌을 때, 각 행과 열의 순서는 해당 도시, 그리고 각 원소는 $i$번째 도시에서 $j$번째 도시까지의 이동 거리를 의미한다. 즉, $C_{31}$은 3번 도시에서 1번 도시까지 거리가 15라는 의미다.

상태, 행동에 대한 정의
먼저 재귀식을 도출하기 위해 상태와 행동을 정의해보자. 상태는 최단 경로와 유사하게 현재 어떤 도시에 있는가가 될 것이다. 그런데, 상태는 의사결정을 내리기 위해 필요한 최소한의 정보를 의미한다는 점을 되짚어봤을 때, 이 한 가지 정보만으로는 의사결정을 내릴 수 없다. 왜냐하면, 이전에 방문한 도시는 다시 방문하면 안된다는 요구조건이 있기 때문이다. 따라서, 어떤 도시에 방문했었는가라는 추가적인 정보가 필요하다. 즉, 상태는 다음과 같이 $N$과 $n$으로 정의할 수 있다.

다음은 행동을 정의해야 한다. 행동은 현재 도시에서 방문하지 않은 도시들 중 어떤 도시에 방문할지를 결정하는 것이다. 즉, 현재 $n$에 위치하고, 이전에 $N$에 속하는 도시에 방문했다고 했을 때 다음에 방문할 도시 $n^`$은 다음과 같이 정의할 수 있다. 여기서, $IN=\{1,2,3,4\}$은 전체 도시 집합을 의미한다.
$$n^{`} \in IN-(N\cup{\{n\}})$$
재귀식을 통한 가치 함수 결정
앞서 정의한 상태와 행동을 기반으로 가치 함수를 결정해보자. 가치 함수는 $v(N,n)$으로 표현할 수 있으며, 의미는 $N$에 속하는 도시를 방문하였고, 현재 $n$에 위치해 있을 때 방문하지 않은 나머지 도시를 방문하고 다시 원점으로 돌아가는 데 걸리는 최소 거리라고 할 수 있다.
$$v(N,n) = \underset{n^`}{\min}\{r(n, n^`) + v(N\cup\{n\},n^`)\}$$
여기서, $r(n, n^`) + v(N\cup\{n\},n^`)$은 현재 위치 $n$에서 $n^`$을 통해 원점을 돌아가는 데 걸리는 최소시간이며, 이를 최소화하는 $n^`$을 선택하는 문제로 귀결된다.
문제 해결
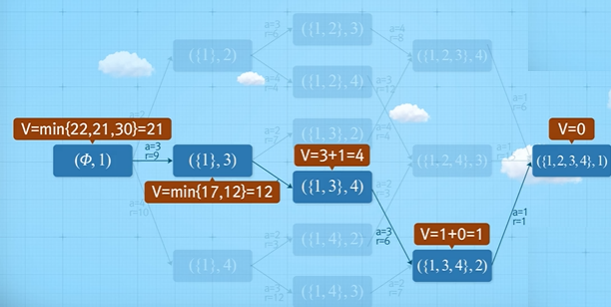
방문판매원 문제의 가능한 모든 상태($N$, $n$)는 다음과 같다.

마찬가지로 가장 작은 문제부터 풀어보면 다음과 같이 계산할 수 있다.

그 이전 단계도 마찬가지로 계산할 수 있다.


따라서 최단 경로는 다음과 같다.
'Reinforcement Learning > 강화학습의 수학적 기초와 알고리듬 이해' 카테고리의 다른 글
| Week6. MDP-2 (0) | 2022.04.03 |
|---|---|
| Week5. MDP-1 (0) | 2022.04.01 |
| Week4. 마르코프 과정 (0) | 2022.03.31 |
| Week2. 동적계획법1 (0) | 2022.03.27 |
| Week1. 강화학습의 이해 (0) | 2022.03.23 |