| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- pinecone
- chat_history
- 추천시스템
- 강화학습의 수학적 기초와 알고리듬 이해
- rl
- langgrpah
- adaptive_rag
- 밑바닥부터시작하는딥러닝 #딥러닝 #머신러닝 #신경망
- summarize_chat_history
- Docker
- rag
- LangChain
- 강화학습의 수학적 기초와 알고리듬의 이해
- Python
- 강화학습
- tool_call_chunks
- tool_calls
- Ai
- toolnode
- RecSys
- fastapi
- subgraph
- update_state
- add_subgraph
- agenticrag
- conditional_edges
- removemessage
- langgraph
- REACT
- 밑바닥부터 시작하는 딥러닝
- Today
- Total
타임트리
Week1. 강화학습의 이해 본문
강화학습: 주어진 상황(state)에서 보상(reward)을 최대화할 수 있는 행동(action)에 대해 학습하는 것
1. 강화학습의 특징
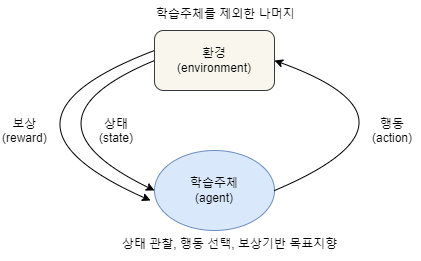
- 학습주체(agent)는 환경에 대한 정보를 모르는 상태에서 학습하기 때문에 특정 상황에서 적합한 행동을 찾기까지는 수많은 시행착오(trial & error)가 필요함
- 현재 선택한 행동이 미래의 순차적 보상에 영향을 미침(delayed reward)
2. Multi-armed Bandit 문제

강화학습의 모든 구성요소를 가지고 있지는 않지만, Multi-armed Bandit 문제를 통해 강화학습의 메커니즘을 간단히 이해해보자. 여러 대의 bandit machine이 있고 행동의 개수가 $k$로 정해진 상황에서 보상을 최대화하기 위해 어떤 행동을 취해야하는지 푸는 문제를 살펴보자. 주어진 상황은 아래와 같다.
- 각 bandit machine에 대한 상태(state) 정보는 부재
- 행동(action)에 대한 즉각적인 보상(reward)
- 목표: $k$개의 bandit machine이 있는 상황에서 보상을 최대화하기 위한 bandit machine 선택
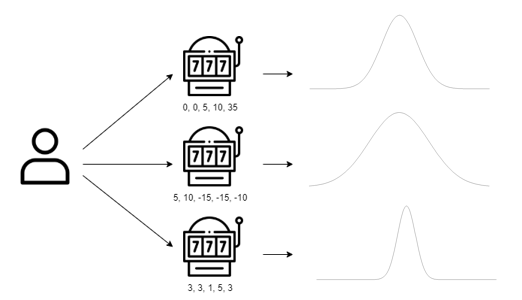
어떤 bandit machine A는 평균적인 보상은 적지만, 그 편차가 작을 수 있고, bandit machine B는 평균 보상은 높으나, 그 편차가 클 수도 있다. 누군가에게 위와 같은 문제를 해결하라고 주어진다면, 일반적으로는 다음과 같은 절차를 따를 것이다.
1. 랜덤하게 시도해보며 각 bandit machine의 보상의 분포를 탐색
2. 경험치가 어느정도 쌓이면, 평균적인 보상이 높은 bandit machine을 선택
1번처럼 강화학습 분야에서 시행착오를 거쳐 어떤 행동이 가장 좋을지 찾는 과정을 탐색(exploration)이라고 한다. 하지만 탐색만을 무한정할 수는 없다. 어느정도 학습이 이루어지고 나서는 보상을 최대화하도록 행동을 취해야 한다. 따라서, 2번과 같이 누적된 정보를 바탕으로, 가장 좋을 것이라 판단되는 행동을 선택하는 것을 활용(exploitation)이라고 한다. 즉, 일반적인 강화학습은 탐색과 활용의 trade-off를 가지고 학습한다.
3. 행동 가치(action values)
행동 가치는 특정 시점(t)에서 어떠한 행동을 취했을 때의 보상에 대한 조건부 기댓값을 말하며,수식으로는 다음과 같다.
$$q(a) = E[R_t|A_t = a] = \sum_{r}{p(r|a)r}$$
여기서, $r$은 보상, $p(r|a)$는 행동 $a$시 보상 $r$의 확률을 의미한다.
학습주체는 각 행동에 대한 보상의 분포(reward distribution)을 모르기 때문에 행동 가치가 학습주체의 의사결정의 지표가 된다. 만약 분포를 알고 있다면, 굳이 시행착오를 겪을 필요 없이 기댓값이 가장 높은 action을 취하면 된다. 하지만, 보상 분포를 모르기 때문에 행동 가치함수를 일련의 시행착오를 통해 보상 분포를 추정하고 이를 바탕으로 행동 가치를 추정하여 가장 좋은(조건부 기댓값이 높은) 행동을 선택한다.
아래 예시 그림을 보면 이해가 더 쉬울 것이다.
그러나 대부분의 경우 최적의 행동 가치에 대한 정보가 부재 상태이다. 그렇다면 어떤 방법으로 행동 가치(기댓값)를 추정할 것인가에 대한 고민이 필요하다. 가장 직관적인 방법은 표본평균의 방법을 이용하는 것이다. 표본평균 방법의 수식은 다음과 같다.
$$Q_t (a)=\frac{1}{n}\sum_{i=1}^n{R_i}$$
분모는 t시점까지 행동 a를 선택한 횟수를 의미하며, 분자는 t시점까지 행동 a를 선택 시 취득한 보상 합을 의미한다. 취할 수 있는 행동의 개수가 3개($k=3$)이며 치료가 성공하면 보상이 1, 아니면 0인 임상시험 예시를 살펴보자.
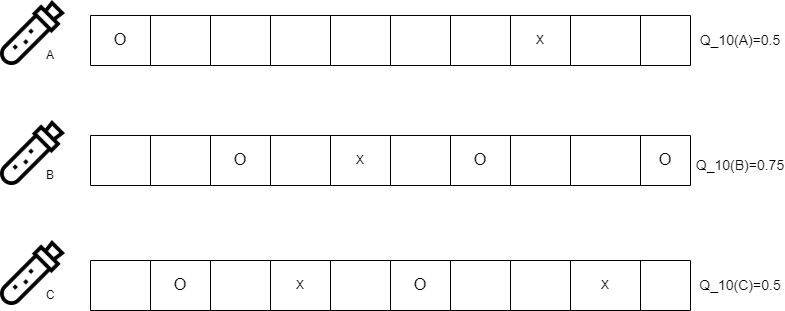
만약 위 정보를 바탕으로 11번째 action을 선택한다면(활용; exploitation), 행동 가치에 따라서 B약을 선택할 것이다.
4. 증분 업데이트 규칙(Incremental update rule)
행동 가치 추정치 $Q_t(a)$를 보다 효율적으로 계산하기 위해 다음과 같이 식을 다시 써보자.
$$Q_{n+1} = \frac{1}{n}\sum_{i=1}^n{R_i} = \frac{1}{n}(R_n + \sum_{i=1}^{n-1}R_i)= \frac{1}{n}(R_n + \frac{n-1}{n-1}\sum_{i=1}^{n-1}R_i))$$
$$ = \frac{1}{n}(R_n + (n-1)Q_n) = Q_n + \frac{1}{n}(R_n - Q_n)$$
즉 행동 가치 추정치는 다음과 같이 기존의 정보($Q_n$)와 새로운 정보와 기존 정보의 차이($R_n-Q_n$)으로 이루어진 형태로 나타낼 수 있다.
$$Q_{n+1} = Q_n + \frac{1}{n}(R_n - Q_n)$$
위 식의 의의는 보상의 합을 매번 계산하는 것이 아니라, $Q$값을 계속 추적한다는 것이다. 즉, $n+1$번째 $Q_{n+1}$을 계산하기 위해서 이 전의 값들을 모두 저장해놓을 필요 없이 $n$번째의 $Q_{n}$의 값만 필요하다.
5. 비정상성 문제(Nonstationary)
위 식을 다시 한 번 살펴보면, 모든 단계의 보상 가중치를 동일하게 주고 있다는 것을 알 수 있다. 그러나 때로는 시간에 따라 보상의 가치가 달라질 수도 있는데, 이를 비정상성 상황이라고 한다. 만약 우측 식 두 번째 항의 $\frac{1}{n}$을 변경한다면 시간에 따라 다른 가중치를 부여할 수 있다. 이를 Step-size 인자 조절 방식이라고 한다.
$$Q_{n+1} = Q_n + a_n(R_n - Q_n) = a_n R_n + (1-a_n)Q_n$$
6. 정보(추정치)의 업데이트 방식
정보 또는 추정치를 업데이트하는 많은 경우, 위와 같은 방식을 취한다. 즉, 기존 추정치에 새로운 정보와 기존 정보와의 차이만큼을 $\alpha$라는 가중치만큼 반영하는 것이다(혹은 기존 정보와 새로운 정보의 가중평균).
$$V = V + \alpha(\hat{V} - V)$$
$$= (1-\alpha)V + \alpha\hat{V}$$
7. 강화학습 맛보기 - <Q-Learning>
강화학습이 어떻게 이루어지는지 Q-Learning을 통해 간단히 알아보자. 지금은 Q-Learning을 단순화하여 살펴보기로 하고, 추후 자세히 학습하자. Q-Learning에서 정보를 순차적으로 업데이트하는 수식은 다음과 같다.
$$Q(s_t, a_t) := (1-\alpha)Q(s_t,a_t) + \alpha(r_{t+1} +\gamma~max_{a}Q(s_{t+1},a))$$
이때 $Q(s_t,a_t)$는 state $s_t$에서 action $a_t$를 선택 시 얻을 수 있는 최대 누적 보상의 기대치를 의미하며 이는 위 식에서처럼 기존 정보 $Q(s_t,a_t)$와 새로운 정보($\hat{Q}(s_t,a_t) = r_{t+1} +\gamma~max_{a}Q(s_{t+1},a)$)의 가중평균으로 볼 수 있다.
보다 문제를 쉽게 만들기 위해 $\alpha=1, \gamma=1$을 가정해보자. 그럼 기존 정보는 고려하지 않고 새로운 정보만을 받아들이며, 이때 새로운 정보는 즉각적인 보상($r_{t+1}$)과 다음 상태에서 얻을 수 있는 최대 누적 보상($max_{a}Q(s_{t+1},a)$)으로 이루어진다.
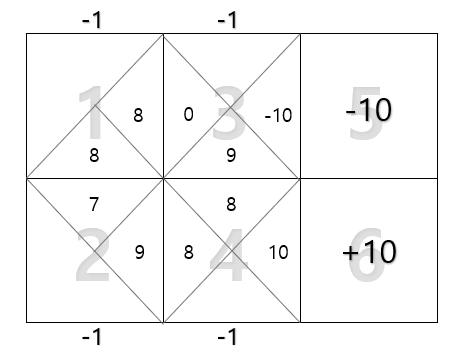
이해를 위해 아래의 1~6으로 이루어진 그리드 월드(grid world)를 살펴보자. 여기에서 1칸에서 시작해 5칸 혹은 6칸으로 도착할 때 종료되는 로봇을 학습시키고자 하는데, 로봇은 그리드에 대한 정보를 가지고 있지 않다. 목표는 어떤 경로로 이동해야 최대 누적 보상을 얻는지를 학습시키는 것이다.
각 그리드별로 2개 혹은 3개의 의사결정을 내릴 수 있으며, state $s_t$는 로봇의 현재 위치(1,2,3,4,5,6)를 나타낸다. 또한, action $a_t$는 화살표로 나타내며, 그리드 내 삼각형 안의 숫자는 $Q(s,a)$를 나타낸다. 그리고 1,2,3,4번 그리드의 보상은 -1, 5번은 -10, 6번은 +10이다.
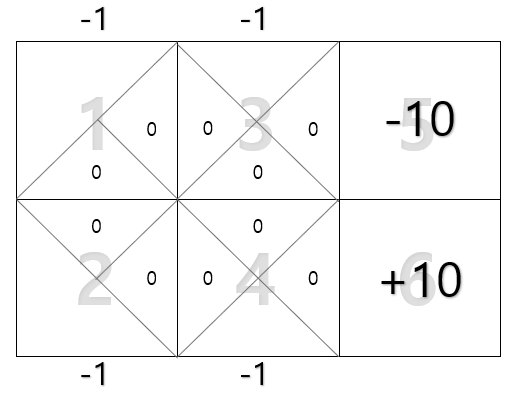
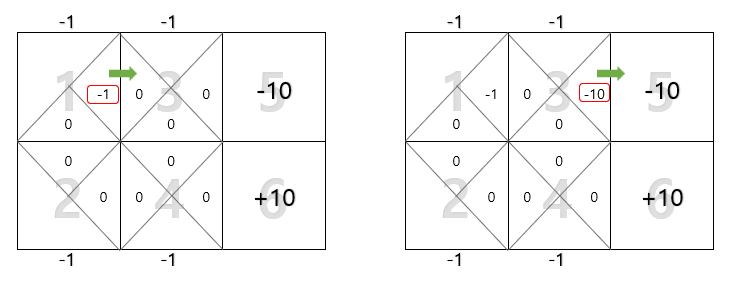
예를 들어, 첫 번째 에피소드가 ($s_t$, $a_t$): (1, →), (3, →) (5, )라고 해보자(한 번의 종료가 일어날 때까지의 학습을 에피소드라고 한다). 그럼 다음과 같이 업데이트 되어진다. 가장 첫번째 시점에서 -1이 계산되는 과정을 살펴보면, 3번 셀을 선택함으로써 -1($r$)의 보상을 얻고, 다음 state인 3번 셀에서 얻을 수 있는 최대 누적 보상합은 0이므로 -1로 계산된다.
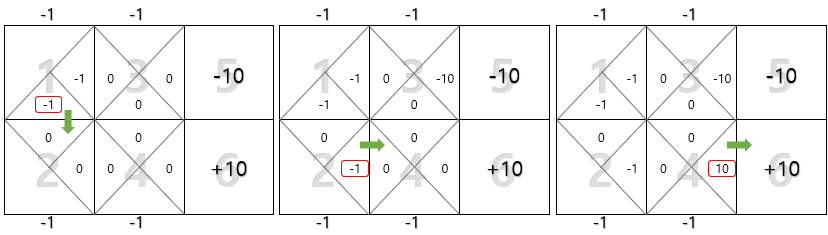
두 번째 에피소드는 ($s_t$, $a_t$): (1, ↓), (2, →), (4, →), (6, ) 라고 하자. 그럼 마찬가지로 아래와 같은 과정을 거쳐 Q값들이 갱신될 것이다.
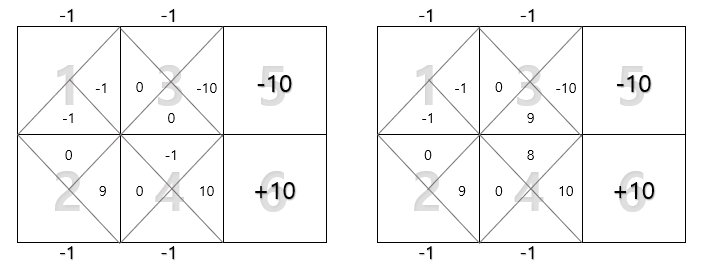
다음 에피소드는 ($s_t$, $a_t$): (1, ↓), (2, →), (4, ↑), (3, →), (5, )와 (1, →), (3, ↓), (4, ↑), (3, →), (5, ) 라고 하자. 그 결과는 다음과 같다.
마지막 에피소드는 ($s_t$, $a_t$): (1, ↓), (2, →), (4, ←), (2, ↑), (1, →), (3, →), (5, ) 라고 하자. 그 결과는 다음과 같다.
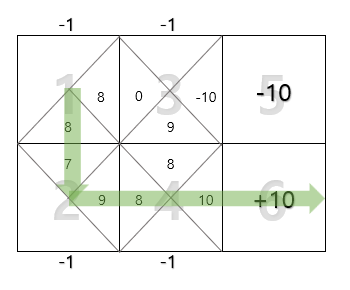
학습이 끝난 뒤, 누적 보상합을 최대화하는 경로를 그려보면 다음과 같다.
'Reinforcement Learning > 강화학습의 수학적 기초와 알고리듬 이해' 카테고리의 다른 글
| Week6. MDP-2 (0) | 2022.04.03 |
|---|---|
| Week5. MDP-1 (0) | 2022.04.01 |
| Week4. 마르코프 과정 (0) | 2022.03.31 |
| Week3. 동적계획법2 (0) | 2022.03.29 |
| Week2. 동적계획법1 (0) | 2022.03.27 |